Ocean Engineering Laboratory
Department of Mechanical Systems Engineering
■ Example 4 : Simulation of the flow around a planing hull using the BEM
|
● Why is the BEM used ? In the numerical solution method based on partial differential equations, computed results tend to be easily affected by the choice of numerical scheme and the setting of some computational parameters, while the BEM, which is the method based on integral equations, has much less influence, specially in the wave-making problem for floating body's motions, it is well known that the reliable solutions can be obtained. (e.g. See "The workshop of ISOPE Numerical Wave Tank Group" in https://www.isope.org/conferences/conferences.htm). ● How about the description of wave-breaking or splash ? The employment of Lagrangian manner for the fluid particles on the free surface makes it possible to describe the large deformation of water surface and the plunging breaker computationally. The nonlinear time-domain computational method by using BEM, in which there is no theoretical assumption except for the condition of inviscid and incompressive fluid and irrotational flow, is already achieved, while the stable computation cannot be often realized in the particular problem dealing with fluid motion with large acceleration. The fluid phenomenon for a planing vessel to eject spray is such an example, and generally it's not easy to capture these phenomena in numerical analysis. The local geometric shape of computational domain causes numerical errors and leads to computational breakdown. This is a main reason that method lacks robustness in its application to strongly nonlinear problems, which has been gradually made clear by our research development. As for the liquid breakup which the splash evolution causes, the ordinary approach by the BEM cannot follow the computation because the splash evolution shrinks the fluid area partially and the contact between boundaries leads to computational termination. However, introducing the artificial liquid breakup which has theoretical grounds based on the domain -decomposition method, we can makes long-time computation. ● What is the computational simulation needed for ? The wave-making resistance of a vessel planing beyond the last hump becomes smaller as the speed gets high, while the spray resistance becomes larger. Although the spray generation is inevitable in nature, the attachment of spray rails are known to reduce the resistance actually. The theoretical proof seems to be hard, but if more detailed computational simulation becomes possible in the future, we may be able to discuss the spray resistance of arbitrary hulls from a viewpoint of law of energy conservation. |
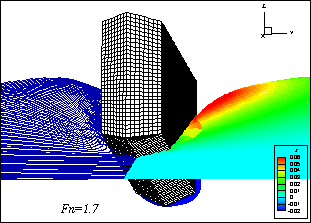
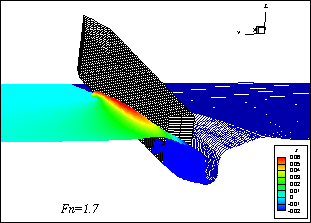
In above two figures, the flow around a prismatic planing hull simulated by the BEM-based 2D+T method, which is a kind of high- speed slender body theory, is shown. The upper is a front view, and the lower, a back one.
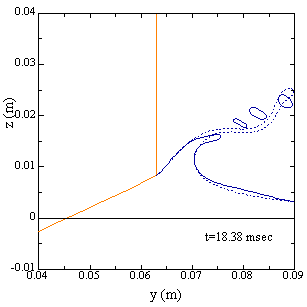
This figure is the computational snapshot of splash ejected from a chine. The numerical model by the artificial liquid breakup is employed in the solid line, and the dotted line is computed by the ordinary method.
|